Như chúng ta đã biết cách đo một góc nhọn của tam giác vuông bằng tỷ số của các cạnh của nó, đã đến lúc tìm hiểu các tỷ số lượng giác đối với bất kỳ góc nào theo số đo radian và nghiên cứu chúng dưới dạng các hàm lượng giác.
Xét một đường tròn bán kính đơn vị có tâm ở gốc tọa độ.
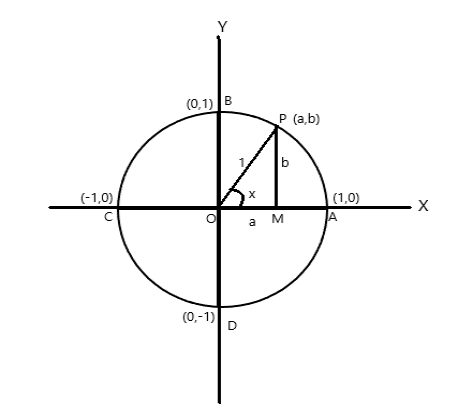
Toạ độ các điểm A = (1,0), B = (0,1), C = (-1,0) và D = (0,-1)
Gọi P(a,b) là một điểm bất kì trên đường tròn có \(\angle AOP = x \) radian. Do đó độ dài cung \(AP = x \) đơn vị.
\(\cos x = a\) , \(\sin x = b\) . Vì \(\bigtriangleup POM\) là tam giác vuông nên \(OP^2 = OM^2 + PM^2\)
do đó \(1 = a^2 + b^2\)
| \(\mathbf{ \cos^2 x + \sin^2x = 1}\) |
Vì một vòng quay hoàn chỉnh làm lệch tâm đường tròn một góc \(2\pi\) radian. Từ hình trên
\(\angle AOB = \pi/2 \)
\(\angle AOC = \pi\)
\(\angle AOD = \frac{3\pi}{2} \)
Ta biết \(\cos x = \frac {\textrm {Base}}{\textrm{Hypotenuse}}\) và \(\sin x = \frac {\textrm {Perpendicular}}{\textrm{Hypotenuse}}\)
\(\cos0^\circ = 1\) \(\sin0^\circ = 0\)
\(\cos\frac{\pi}{2} = 0\) \(\sin\frac{\pi}{2} = 1\)
\(\cos\pi = -1\) \(\sin\pi = 0\)
\(\cos2\pi = 1\) \(\sin2\pi = 0\)
Khi chúng ta đi hết một vòng từ điểm P, chúng ta lại đến điểm P. Giá trị của \(\cos x\) và \(\sin x\) không đổi, do đó chúng ta có thể nói rằng
khi x tăng hoặc giảm theo bội số nguyên của \(2\pi\) , giá trị của hàm sin, cosin không thay đổi. Như vậy,
\(\sin(n\cdot2\pi + x) = \sin x\)
\(\cos(n\cdot 2\pi + x) = \cos x \)
trong đó n là một số nguyên.
Chúng tôi sẽ nhận thấy rằng \(\sin x = 0\) khi \(\space x = n\pi\)
và \(\cos x = 0\) khi \(x = (2n+1)\pi/2\)
Suy ra các hàm lượng giác khác dưới dạng hàm sin và cosin.
| \(\mathbf{\csc x} = \mathbf{\frac{1}{\sin x}}\) trong đó \(x \neq n\pi\) |
| \(\mathbf{\sec x } = \mathbf{\frac{1}{\cos x}}\) trong đó |
| \(\mathbf{\tan x } = \mathbf{\frac{\sin x}{\cos x}}\) trong đó |
| \(\mathbf{\cot x } = \mathbf{\frac{\cos x}{\sin x}}\) trong đó \( x \neq n\pi\) |
| \(\textbf 1 + \mathbf {\tan^2x = \sec^2x}\) |
| \(\textbf 1 + \mathbf {\cot^2x = \csc^2x}\) |
Bảng dưới đây cho thấy dấu và giá trị của các hàm lượng giác thay đổi như thế nào trong các góc tọa độ khác nhau.
| góc phần tư | TÔI | II | III | IV |
| tội lỗi | + | + | - | - |
| cosx | + | - | - | + |
| tanx | + | - | + | - |
| cosecx | + | + | - | - |
| secx | + | - | - | + |
| cũi | + | - | + | - |
Hãy xem bảng dưới đây cho biết giá trị của các góc lượng giác cho các độ như 0°, 30°, 45°, 60° và 90°.
Góc (tính bằng độ & radian) | tội | cos | rám nắng | cũi | csc | giây |
| 0° | 0 | 1 | 0 | ∞ | ∞ | 1 |
| 30° hoặc π/6 radian | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 |
| 45° hoặc π/4 radian | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° hoặc π/3 radian | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 |
| 90° hoặc π/2 radian | 1 | 0 | ∞ | 0 | 1 | ∞ |
| 180° hoặc π radian | 0 | -1 | 0 | ∞ | ∞ | -1 |
| 270° hoặc 3π/2 radian | -1 | 0 | ∞ | 0 | -1 | ∞ |
| 360° hoặc 2π radian | 0 | 1 | 0 | ∞ | ∞ | 1 |
Quan sát bảng trên, bạn sẽ nhận thấy rằng:
\(\mathbf{\sin x = \cos(90^\circ-x)}\) |
| \(\mathbf{\tan x = \cot(90^\circ-x)}\) |
| \(\mathbf{\sec x = \csc(90^\circ-x) }\) |
| \(\mathbf{\csc x = \sec(90^\circ-x)}\) |
| \( \mathbf{ \sin(-x) = -\sin x}\) |
| \( \mathbf{ \cos(-x) = \cos x}\) |
| \(\tan(-x) = -\tan x\) |
Biểu diễn đồ họa của \(\sin x\) và \(\cos x\) trong đó y nằm trong khoảng từ -1 đến +1 khi x nhận các giá trị từ \(-3\pi \) đến \(3\pi \) . Cả hai giá trị sin và cosin của hàm lượng giác đều lặp lại sau một khoảng \(2\pi \) .
Sine được hiển thị dưới dạng đường liền nét và Cosine dưới dạng đường chấm chấm.
Hãy để chúng tôi giải quyết một vài ví dụ dựa trên các hàm lượng giác trên:
Ví dụ 1: Nếu \(\cos x\) = − 4/5, x nằm ở góc phần tư thứ ba, hãy tìm giá trị của năm hàm lượng giác còn lại.
Giải pháp: Tham khảo các bảng được đưa ra ở trên.
Vì \(\cos x\) = -4/5 nên \(\sec x\) = -5/4
Vì \(\mathbf{ \cos^2 x + \sin^2x = 1}\) nên \({16\over25} + \sin^2x = 1 ⇒ \sin^2x = 1-\frac{16}{25} = {9\over25}\)
\(\sin x = \pm3/5\)
Vì x nằm ở giá trị góc phần tư thứ ba nên \(\sin x\) sẽ âm (tham khảo bảng dấu góc phần tư). Do đó \(\sin x\) = -3/5 và \(\csc x \) = -5/3
Vì \(\tan x = \sin x/\cos x\) , nên \(\tan x\) = \(\frac{-4/5}{-3/5}\) = 4/3
Ví dụ 2: Tìm giá trị của \(\cos(5\pi/2)\)
Giải pháp: \(\cos(5\pi/2) = \cos (2\pi + {1\pi}/_2)\)
Vì giá trị của cosine lặp lại sau \(2\pi \) nên \(\cos(2\pi + {1\pi}/_2) = \cos(\pi/2) = 0\)