ဤသင်ခန်းစာသည် ဂဏန်းငယ်များကို တစ်ဝက်ခွဲခြင်းအကြောင်းဖြစ်သည်။
Halfing ဆိုသည်မှာ အညီအမျှ အပိုင်း ၂ ပိုင်းခွဲခြင်း ကို ဆိုလိုသည်။
လိမ္မော်သီးတစ်လုံးယူရအောင်။

ပြီးလျှင် အညီအမျှ နှစ်ပိုင်းဖြတ်ပါ။
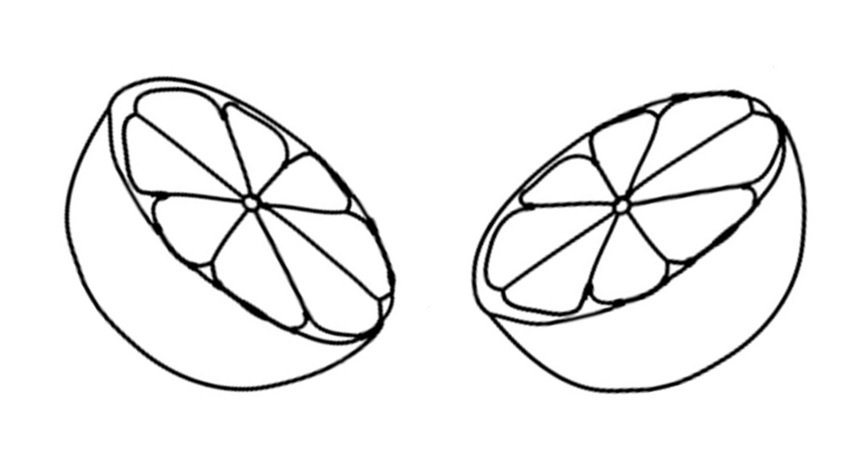
အညီအမျှ ပိုင်းဖြတ်ခြင်းကို 'တစ်ဝက်' ဟု ဆိုလိုသည်။ အစိတ်အပိုင်းတစ်ခုစီသည် လိမ္မော်သီးတစ်လုံး၏ တစ်ဝက်စီဖြစ်သည်။
ပုံသဏ္ဍာန်တစ်ဝက်ကို 'အညီအမျှနှစ်ပိုင်း' ပေးရန်အတွက် ၎င်းကို အလယ်တွင်ခွဲထားကြောင်း သေချာစေရပါမည်။
ဒီစက်ဝိုင်းကို အောက်မှာကြည့်ပါ။ တစ်ဝက်ခွဲထားသလား။
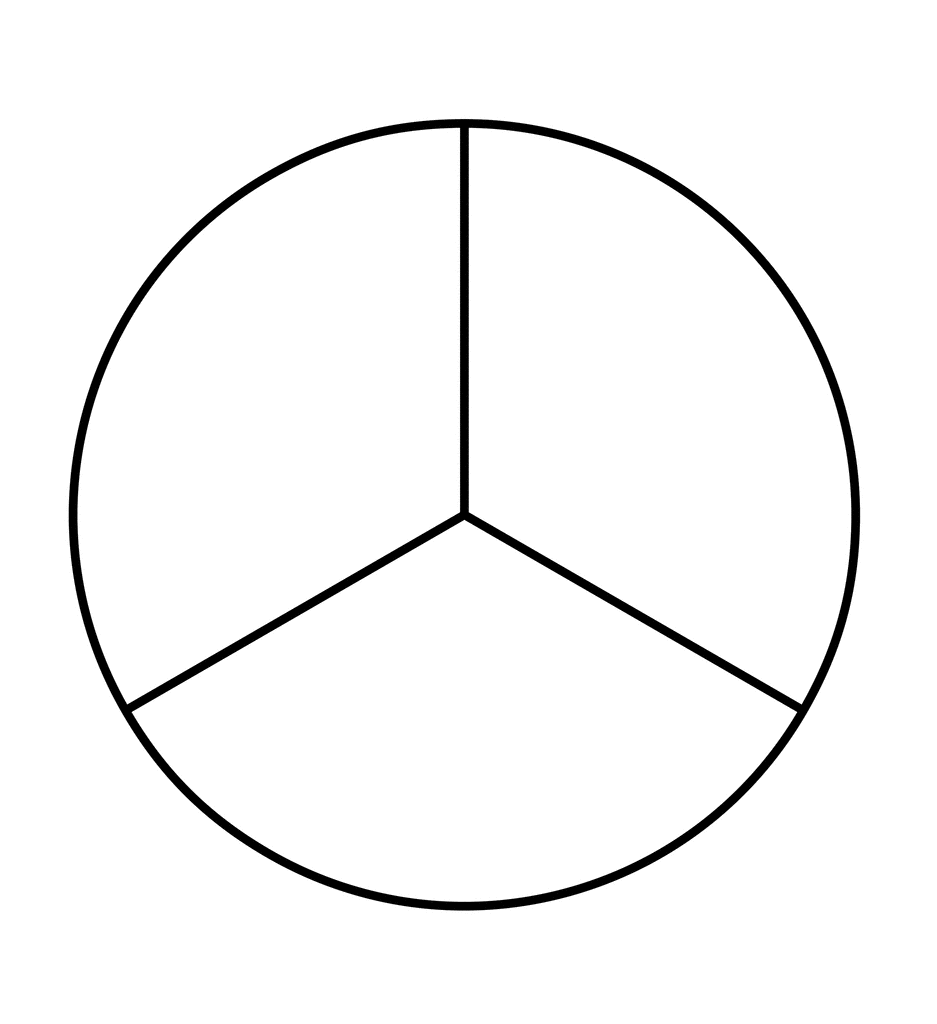
မဟုတ်ဘူး အဘယ်ကြောင့်?
အဘယ်ကြောင့်ဆိုသော် တစ်ဝက်သည် နှစ်ခုကို အညီအမျှ ပိုင်းခြားထားခြင်းကို ဆိုလိုပြီး ဤစက်ဝိုင်းကို TWO မဟုတ်ဘဲ သုံးပိုင်းခွဲထားသောကြောင့် ဖြစ်သည်။ ဒီတော့ ဒါက တစ်ဝက်မဟုတ်ဘူး။
မှတ်သားရန် အလွန်အရေးကြီးသောအချက်မှာ ကျွန်ုပ်တို့သည် ကိန်းဂဏန်းများ တစ်ဝက်စီရသောအခါတွင် ကျွန်ုပ်တို့သည် ဂဏန်းတစ်လုံးလုံးကို ရနိုင်သော်လည်း ဂဏန်းများ ထက်ဝက်တွင် ဂဏန်းများအားလုံးကို ဂဏန်းတစ်လုံးမျှ မဖြစ်စေရပါ။
ပုံသဏ္ဍာန်ထက်ဝက်ဆီသို့ နည်းလမ်းတစ်ခုထက်ပိုပါသည်။
စတုဂံ သို့မဟုတ် စတုရန်းစာရွက်ကို ယူပါ။ တတ်နိုင်သမျှ တစ်ဝက်လောက် ဖြတ်နိုင်အောင် ကြိုးစားပါ။
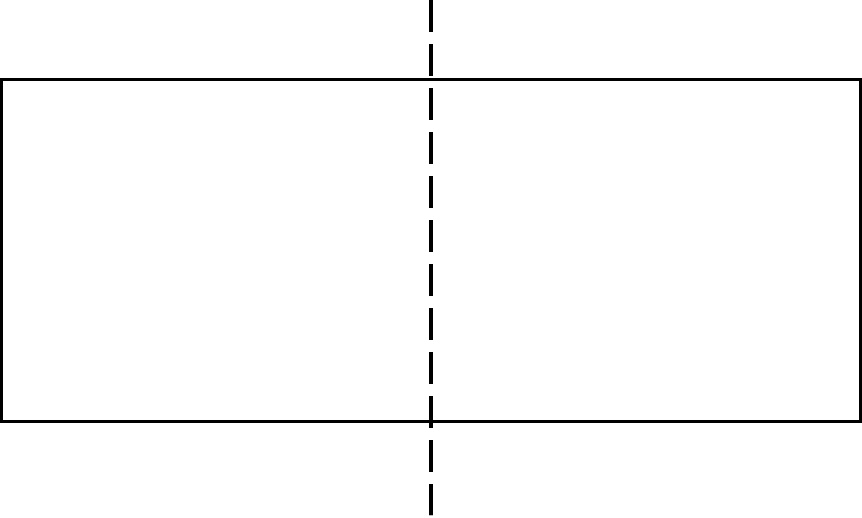
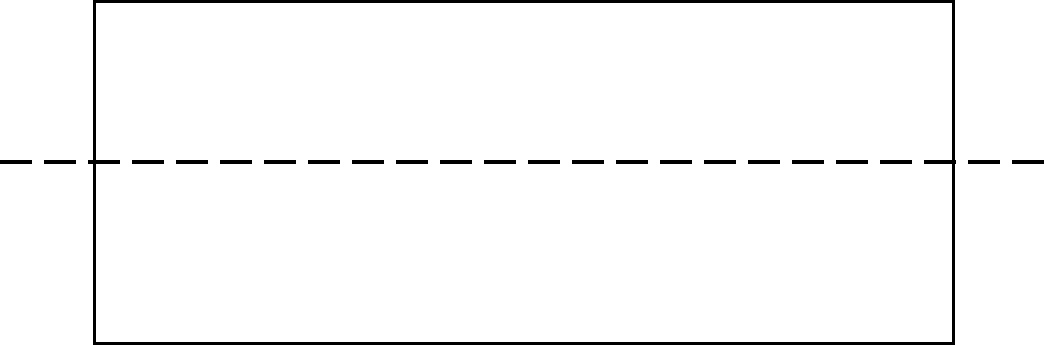
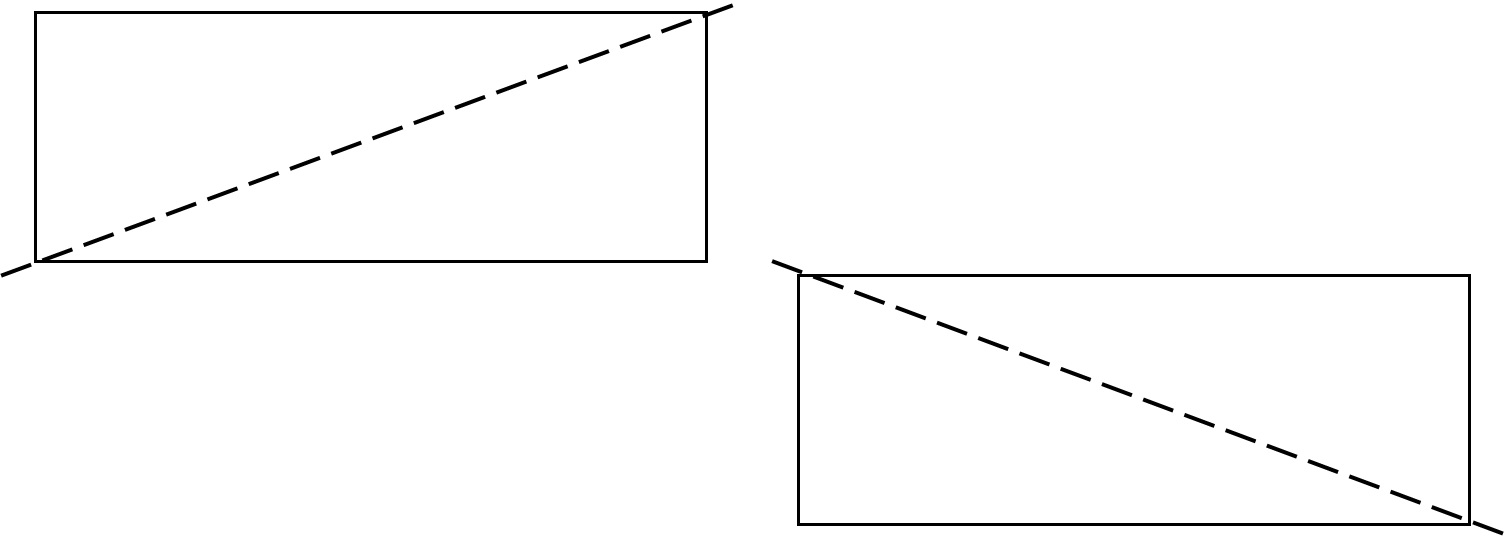
ထို့ကြောင့် တစ်ဝက်စီခွဲ နေသည်ကို သင်မြင်ရသည်- ၎င်းသည် တစ်စုံတစ်ခုကို အညီအမျှ နှစ်ပိုင်းခွဲကာ အပိုင်းတစ်ခုစီကို ' တစ်ဝက်' ဟုခေါ်သည်။
လူနှစ်ယောက်ကြား အညီအမျှ မျှဝေခြင်းဖြင့် နံပါတ်တစ်ဝက်ကို သင်ယူကြပါစို့။
ခြောက်ချောင်းရှိတယ်။
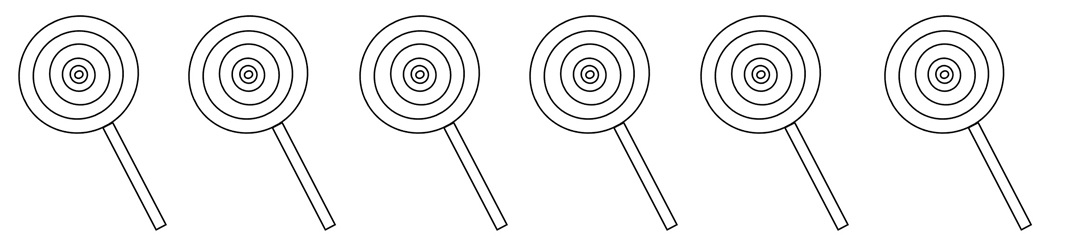
ပေတရုနှင့် ဆမ်တို့ကြား ၎င်းတို့ကို အညီအမျှ ပိုင်းခြားပါ။
ဘေးတစ်ဖက်စီတွင် lollipops အရေအတွက် တူညီစေရန်အတွက် ကြားတွင်မျဉ်းဆွဲပါ။
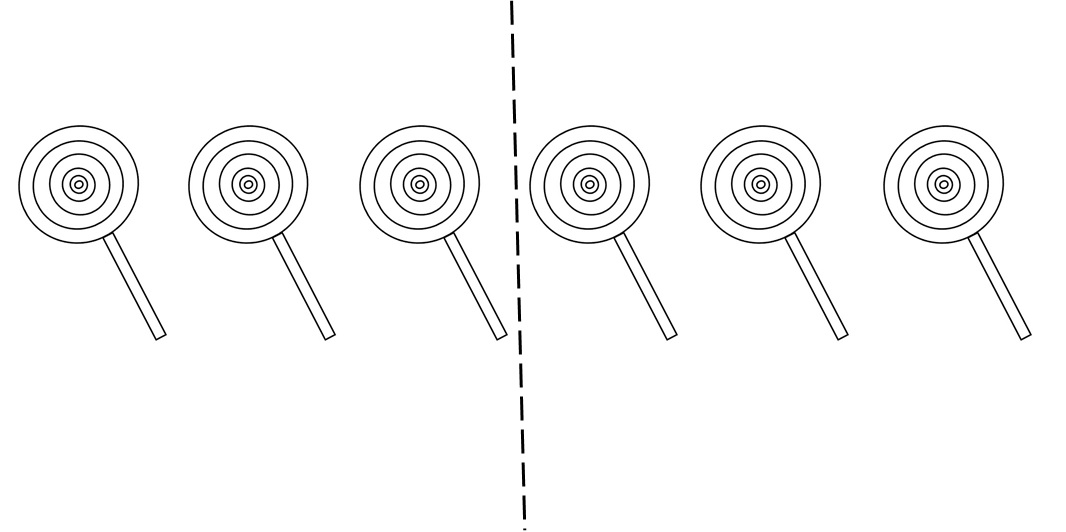
မျဉ်းတစ်ဖက်စီတွင် lollipop 3 ခုရှိသည်
Sam က lollipop 3 ခုရမှာဖြစ်ပြီး Peter က lollipop 3 ခုရပါလိမ့်မယ်။
ဆိုလိုသည်မှာ 6 ၏တစ်ဝက်သည် 3 ဖြစ်သည်။
အောက်ပါစတုရန်းများကို အညီအမျှ နှစ်ပိုင်းခွဲကြည့်ရအောင်။

ဤသည်မှာ 8 စတုရန်းများဖြစ်သည်။ 8 ၏ တစ်ဝက်သည် ______________ ဖြစ်သည်။
ဂိမ်းလေးတစ်ခု ကစားကြရအောင်။ သင့်မိဘ သို့မဟုတ် သူငယ်ချင်းနှင့် ဤဂိမ်းကို ကစားရခြင်းသည် ပျော်စရာကောင်းလိမ့်မည်။
စက္ကူတစ်ရွက်ကို အတုံးသေးသေး 20 ပိုင်းဖြတ်ပါ။
1. 10 အပိုင်းကိုထည့်ကာ ကစားသမားနှစ်ဦးစလုံးကြား အညီအမျှမျှဝေပါ။
ဘယ်နှစ်ကောင် ရခဲ့လဲ။ 5 လား။
တခြားကစားသမားက ဘယ်နှစ်ထည်ရလဲ။ 5 လား။
ဒီတော့ 10 ရဲ့ တစ်ဝက်က 5 ဖြစ်ပါတယ်။
2. အပိုင်း 16 ပိုင်းထည့်ကာ ကစားသမားနှစ်ဦးစလုံးကြား အညီအမျှ မျှဝေပါ။ တစ်ခုစီ ဘယ်နှစ်ကောင် ရခဲ့လဲ။
(အဖြေ - ၈ခုစီ)
3. အပိုင်း 20 ကိုထည့်ကာ ကစားသမားနှစ်ဦးစလုံးကြား အညီအမျှ မျှဝေပါ။ တစ်ခုစီ ဘယ်နှစ်ကောင် ရခဲ့လဲ။
(အဖြေ - 10 ကျပ်စီ)
ကောင်းပြီ၊ ယခု အောက်ပါ နံပါတ်များ၏ တစ်ဝက်ကို ချရေးပါ။
2 ၏တစ်ဝက်သည် ___________
4 ၏တစ်ဝက်သည် ___________
6 ၏တစ်ဝက်သည် ___________
8 ၏တစ်ဝက်သည် ___________
10 ၏တစ်ဝက်သည် ___________
12 ၏တစ်ဝက်သည် ___________
၁၄ ၏တစ်ဝက်သည် ___________
16 ၏တစ်ဝက်သည် ___________
18 ၏တစ်ဝက်သည် ___________
20 ၏တစ်ဝက်သည် ___________
သင့်အဖြေများသည် အောက်ပါအတိုင်းဖြစ်ပါသလား။
2 ၏တစ်ဝက်သည် 1 ဖြစ်သည်။
4 ၏တစ်ဝက်သည် 2 ဖြစ်သည်။
6 ၏တစ်ဝက်သည် 3 ဖြစ်သည်။
8 ၏တစ်ဝက်သည် 4 ဖြစ်သည်။
10 ၏တစ်ဝက်သည် 5 ဖြစ်သည်။
12 ၏တစ်ဝက်သည် 6 ဖြစ်သည်။
14 ၏တစ်ဝက်သည် 7 ဖြစ်သည်။
16 ၏တစ်ဝက်သည် 8 ဖြစ်သည်။
18 ၏တစ်ဝက်သည် 9 ဖြစ်သည်။
20 ၏တစ်ဝက်သည် 10 ဖြစ်သည်။
Halfing သည် Doubling ၏ဆန့်ကျင်ဘက်ဖြစ်သည်။ ဥပမာအားဖြင့်၊ 2 ၏နှစ်ဆသည် 4 ဖြစ်ပြီး 4 ၏တစ်ဝက်သည် 2 ဖြစ်သည်။
10 ၏တစ်ဝက်သည် 5 ဖြစ်သည်ကိုမှတ်သားထားရန်ကောင်းလိမ့်မည်။
ထို့ကြောင့်၊ 20 ထက်ကြီးသောမည်သည့်ဂဏန်းအတွက်မဆို ၎င်းတို့ကို ဆယ်ဂဏန်းနှင့်တစ်ခုအထိ စီမံနိုင်သောအပိုင်းများအဖြစ် ခွဲနိုင်ပြီး နှစ်ခုကြား အညီအမျှ မျှဝေနိုင်သည်။
ဥပမာအားဖြင့်၊ 24 ကို တစ်ဝက်ခွဲရန်၊ ကျွန်ုပ်တို့သည် နံပါတ်ကို ပိုင်းခြားပြီး နံပါတ်တစ်ခုစီ၏ တစ်ဝက်စီကို ရှာပါမည်။
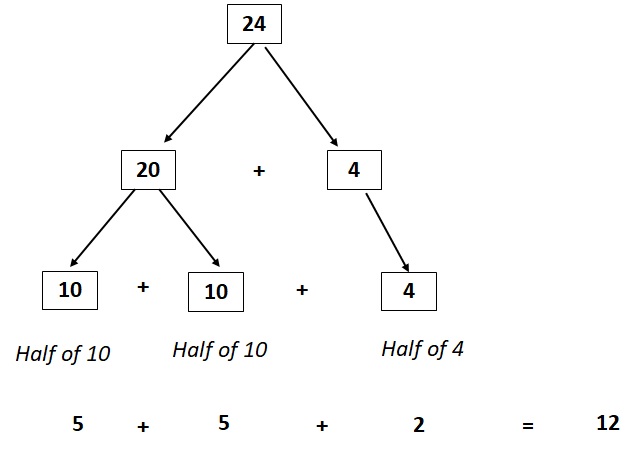
24 = 10 + 10 + 4
10 ၏တစ်ဝက်သည် 5 ဖြစ်ပြီး 4 ၏တစ်ဝက်သည် 2 ဖြစ်သည်။
ဒီတော့ 24 ရဲ့ တစ်ဝက်က 10 ရဲ့ တစ်ဝက် + 10 ရဲ့ တစ်ဝက် + 4 = 5 + 5 + 2 = 12၊
ဂဏန်းတွေအတွက် ဒီနည်းလမ်းကို လေ့ကျင့်ကြည့်ရအောင်။
1. 30 ၏တစ်ဝက်ကိုရှာပါ။
နံပါတ်ကိုခွဲခြမ်းပြီး နံပါတ်တစ်ခုစီ၏ တစ်ဝက်ကို ရှာပါ။
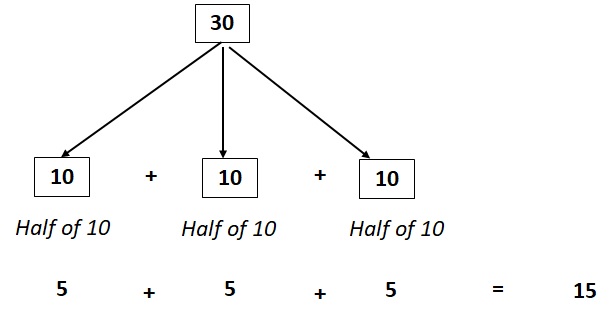
30 = 10 + 10 + 10
30 = 5 + 5 + 5 = 15 တစ်ဝက်
2. 36 ၏တစ်ဝက်ကိုရှာပါ။
နံပါတ်ကိုခွဲခြမ်းပြီး နံပါတ်တစ်ခုစီ၏ တစ်ဝက်ကို ရှာပါ။
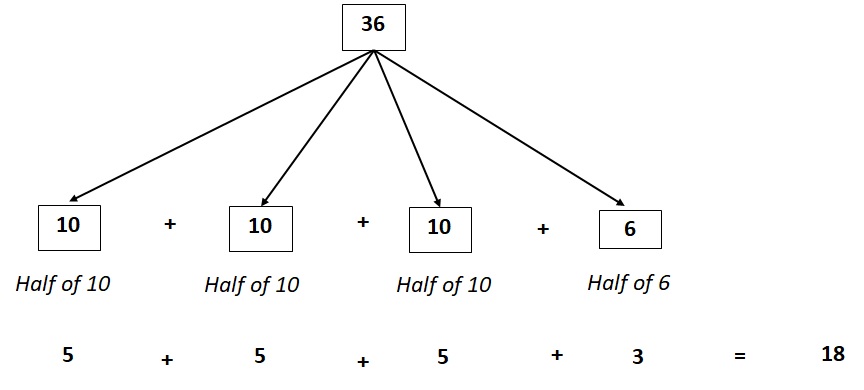
၃၆ = ၁၀+၁၀+၁၀+၆
10 ၏တစ်ဝက်သည် 5 ဖြစ်ပြီး 6 ၏တစ်ဝက်သည် 3 ဖြစ်သည်။
36 = 5 + 5 + 5 + 3 = 18 တစ်ဝက်
3. 48 ၏တစ်ဝက်ကိုရှာပါ။
နံပါတ်ကိုခွဲခြမ်းပြီး နံပါတ်တစ်ခုစီ၏ တစ်ဝက်ကို ရှာပါ။
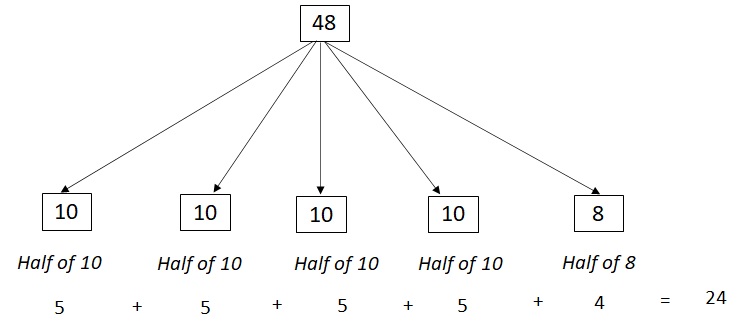
၄၈ = ၁၀+၁၀+၁၀+၁၀+၈
10 ၏တစ်ဝက်သည် 5 ဖြစ်ပြီး 8 ၏တစ်ဝက်သည် 4 ဖြစ်သည်။
48 = 5 + 5 + 5 + 5 + 4 = 24 တစ်ဝက်
အောက်ပါကိန်းဂဏန်းများကို ထက်ဝက်ခွဲ၍ လေ့ကျင့်ပါ။